In this session, we discussed how the second part of variable environment and Chesson’s coexistence theory.

Materials

The video record of the seminar can be found HERE.

The slides can be found HERE.

The Mathematica notebook is HERE.

Competitive exclusion principle

The first version of the competitive exclusion principle was worded as :

CEP v1.0: No more species can coexist than limiting resources.

However, this principle is often confronted with observation that many more species can coexist on a limited range of resource. Hutchinson proposed the famous paradox of plankton, questioning the prediction of competitive exclusion principle. In fact, one scenario is that many species can coexist before the ecosystem reaches the equilibrium. The competitive exclusion principle was then revised to:

CEP v2.0: No more species can coexist than limiting resources at equilibrium (Armstrong & McGehee 1980 Am Nat)

Even though, the ecosystem at equilibrium can still hold many species in a variable environment.

Chesson’s modern coexistence theory

To make Hutchinson’s argument rigorous, Chesson proposed a modern coexistence theory (Chesson 1994, 2000). The theory is based on the idea that the environment is variable. Two ways of temporal variation can allow species coexistence

Relative nonlinearity

Relative nonlinearity serves as a mechanism promoting species coexistence, arising from the diverse nonlinear growth responses of species to environmental conditions, notably resources. This variance in nonlinear responses induces shifts in the competitive hierarchy across different environmental contexts.

Storage effect

Superior competitor depends on environmental factor that fluctuates over time.

Relative nonlinearity

#| standalone: true
#| viewerHeight: 800
#| viewerWidth: 900
library(shiny)
library(bslib)
library(plotly)
library(Matrix)

growth_rate <- function(mu_max,k, R){
  return(mu_max * R / (R + k))
}


Sim_rc <- function(tt, mu11, mu12, mu21, mu22,
                   k11,k12,k21,k22,
                   v11, v12, v21, v22,
                   r1in, r2in,
                   N10, N20, R10, R20,
                   m,
                   mode) {
  N1 <- c(N10)
  N2 <- c(N20)
  R1 <- c(R10)
  R2 <- c(R20)
  for(ti in 1:tt){
    temp_N1 <- N1[ti]
    temp_N2 <- N2[ti]
    temp_R1 <- R1[ti]
    temp_R2 <- R2[ti]
    for(tii in 1:100){
      if(mode == "ess"){
        mu1 <- min(growth_rate(mu11, k11, temp_R1), growth_rate(mu12, k12, temp_R2))
        mu2 <- min(growth_rate(mu21, k21, temp_R1), growth_rate(mu22, k22, temp_R2))
        c11 <- min(growth_rate(v11, k11, temp_R1), growth_rate(v12, k12, temp_R2))
        c12 <- min(growth_rate(v11, k11, temp_R1), growth_rate(v12, k12, temp_R2))
        c21 <- min(growth_rate(v21, k21, temp_R1), growth_rate(v22, k22, temp_R2))
        c22 <- min(growth_rate(v21, k21, temp_R1), growth_rate(v22, k22, temp_R2))
        
      } else {
        mu1 <- growth_rate(mu11, k11, temp_R1) + growth_rate(mu12, k12, temp_R2)
        mu2 <- growth_rate(mu21, k21, temp_R1) + growth_rate(mu22, k22, temp_R2)
        c11 <- v11 * temp_R1
        c12 <- v12 * temp_R2
        c21 <- v21 * temp_R1
        c22 <- v22 * temp_R2
      }
      
      dN1 <- (mu1 - m) * temp_N1 / 100
      dN2 <- (mu2 - m) * temp_N2 / 100
      dR1 <- ((r1in - temp_R1) - c11 * temp_N1 - c21 * temp_N2) / 100
      dR2 <- ((r2in - temp_R2) - c12 * temp_N1 - c22 * temp_N2) / 100
      
      temp_N1 <- max(temp_N1 + dN1, 0)
      temp_N2 <- max(temp_N2 + dN2, 0)
      temp_R1 <- max(temp_R1 + dR1, 0)
      temp_R2 <- max(temp_R2 + dR2, 0)
      
    }
    
    N1 <- c(N1, temp_N1)
    N2 <- c(N2, temp_N2)
    
    R1 <- c(R1, temp_R1)
    R2 <- c(R2, temp_R2)
  }
  return(data.frame(N1 = N1, N2 = N2, R1 = R1, R2 = R2, cc = 1:(tt+1)))
  
}


# Define UI for app that draws a histogram ----
# Define UI for app that draws a histogram ----
ui <- fluidPage(
  headerPanel(''),
  
  fluidRow(
    column(12, 
           textOutput("text"),
           tags$head(tags$style("#text{color: black;
                                 font-size: 30px;
                                 font-style: italic;
                                 }"
           )
           ),
           plotlyOutput("plot1", width=700, height=260),
           plotlyOutput("plot2", width=700, height=260)
    )
  ), 
  
  fluidRow(
    column(4, 
           div(style="height: 80px;",sliderInput('mu1max', HTML("&mu;<sub>1,max</sub>"), 1.4, min = 0.1, max = 2)),
           div(style="height: 80px;",sliderInput('mu2max', HTML("&mu;<sub>2,max</sub>"), 0.8, min = 0.1, max = 2))
    ),
    column(4,
           div(style="height: 80px;", sliderInput('k1', HTML("K<sub>1</sub>"), 2.3, min = 0.1, max = 3)),
           div(style="height: 80px;",sliderInput('k2', HTML("K<sub>2</sub>"), 0.65, min = 0.1, max = 3))
    ),
    column(4,
           div(style="height: 80px;", sliderInput('m', "m", 0.4, min = 0.01, max = 1)),
    )
  )
  
  
)

server <- function(input, output, session) {
  output$text <- renderText({
    "Relative nonlinearity"
  })
  
  
  
  
  # sim lv model
  sim_result <- reactive({
    Sim_rc(100, input$mu1max, 0, input$mu2max, 0,
           input$k1,0, input$k2, 0,
           3 * input$mu1max,  0, 3 * input$mu2max,0,
           10, 10, 0.1, 0.1, 1, 1, input$m,
           "sub")
  })
  # browser()
  
  output$plot1 <- renderPlotly({
      R <- seq(0, 10, 0.01)
      
      mu1 <-reactive({
        growth_rate(input$mu1max, input$k1, R)
      })
      
      
      mu2 <-reactive({
        growth_rate(input$mu2max, input$k2, R)
      })
      
      gr <- data.frame(re = R, mu1 = mu1(), mu2 = mu2())
      # browser()
      p <- plot_ly(data = gr) %>%
        add_trace(x = ~re, y = ~mu1, type = 'scatter', mode = 'lines', name = 'Species 1', line = list(color = '#86C166', width = 4)) %>%
        add_trace(x = ~re, y = ~mu2, type = 'scatter', mode = 'lines', name = 'Species 2', line = list(color = '#42602D', width = 4))
        
      p <- p %>%
        add_segments(y=input$m, yend = input$m, x = 0, xend=10, type = 'scatter', mode = 'lines', name = "m", line = list(color = '#D0104C', width = 2))
   
      # xlim
      p <- p %>% layout(xaxis = list(range = c(0, 4)))
      p <- p %>% layout(xaxis = list(title = "R"),yaxis = list(title = "Growth rate"))
      
      
      
      p
  })
  
  output$plot2 <- renderPlotly({
    
    # browser()
    p <- plot_ly(data = sim_result()) %>%
      add_trace(x = ~cc, y = ~N1, type = 'scatter', mode = 'lines', name = 'Species 1', line = list(color = '#86C166', width = 4)) %>%
      add_trace(x = ~cc, y = ~N2, type = 'scatter', mode = 'lines', name = 'Species 2', line = list(color = '#42602D', width = 4))
    

    # xlim
    # p <- p %>% layout(xaxis = list(range = c(0, 50)),
    #                   yaxis = list(range = c(0, 2)))
    # xlabel
    p <- p %>% layout(xaxis = list(title = "Time"),yaxis = list(title = "Density"))
    
    
    
    
    p
  })

}
# Create Shiny app ----
shinyApp(ui = ui, server = server)

Trade-off: In this scenario, one species exhibits a higher \(\mu_{max}\) but a greater half-saturation rate, resulting in a growth advantage at high resource concentrations but a disadvantage at low resource levels. Conversely, the other species possesses a lower \(\mu_{max}\) and half-saturation rate, allowing it to grow more rapidly at low resource concentrations but with a larger \(R^{\ast}\). This dynamic reflects the trade-off between growth at low versus high resource availability (\(R^{\ast}\) versus \(\mu_{max}\)), commonly referred to as the gleaner-opportunist trade-off.

Mathematically, this trade-off can be represented by the following equations:

\[ \frac{d^2 \mu_2}{d R^2}< \frac{d^2 \mu_1}{d R^2}<0 \]

Neither species likes environmental variation, but species 2 likes it less as its \(\frac{d^2 \mu_2}{d R^2}\) is more negative, which means it suffers from the change of resource more.

Given the mean of the growth rate being expressed in Taylor expansion form:

\[ \overline{\mu(R)} \approx \mu(\bar{R})+\frac{1}{2} Var(R)\frac{d^2\mu}{dR^2} \]

we can use the ZNGI analysis to study the coexistence of two species. The mean of ZNGI in a variable environment is given by:

\[ \overline{\frac{1}{N}\frac{dN}{dt}} = \overline{\mu(R) - m} = \overline{\mu(R)} - m=0 \]

given \(m\) is constant.

Substituting the Taylor expansion of \(\overline{\mu(R)}\) into the equation, we have:

\[ \mu(\bar{R})+\frac{1}{2} Var(R)\frac{d^2\mu}{dR^2} - m = 0. \]

For simplification, we assume a linear growth function \(\mu(\bar{R})=\mu \bar{R}\), we have the ZNGI in a coordinate of \(\mu(\bar{R})\) and \(Var(R)\):

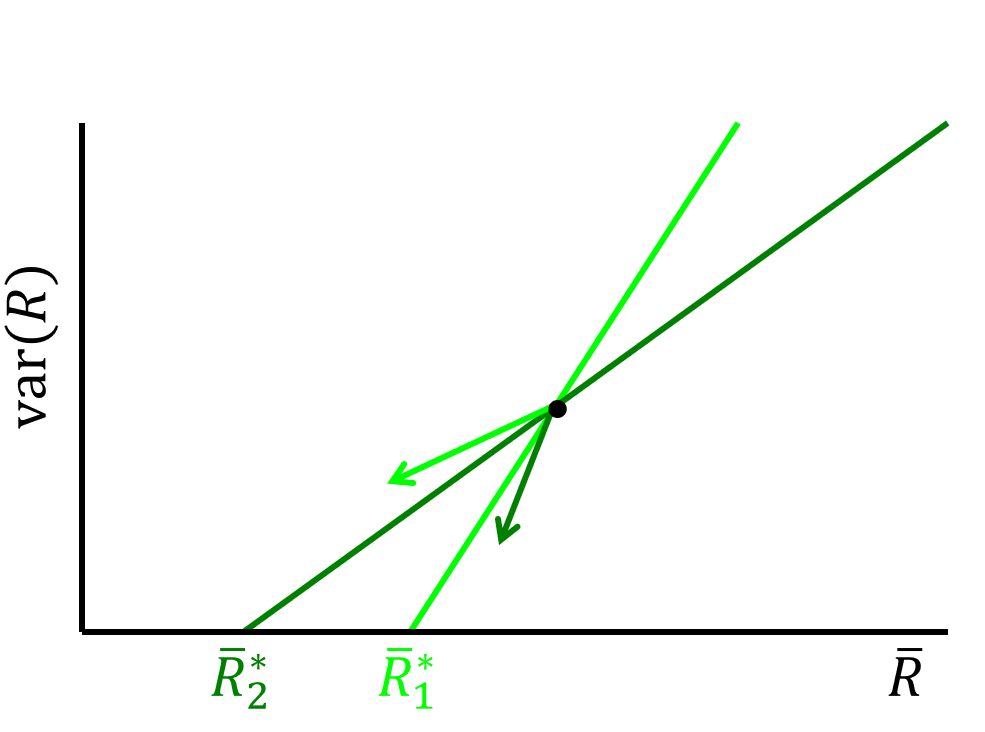
\[ Var(R) = \frac{2}{\frac{d^2\mu}{dR^2}}(m - \mu \bar{R}) \]

The ZNGI is a straight line in the coordinate of \(\mu(\bar{R})\) and \(Var(R)\), with the slope being \(-\frac{2 \mu}{\frac{d^2\mu}{dR^2}}\) and the intercept being \(\frac{2 m}{\frac{d^2\mu}{dR^2}}\).

From the ZNGI analysis, we know that only when two ZNGIs cross in the first quadrant, the coexistence of two species is possible. Thus, the coexistence of two species requires that one should have a larger intercept at \(\bar{R}\) axis and a larger slope (Species 1) while the other should have a smaller intercept and a smaller slope (Species 2) (see the figure below). This is consistent with the trade-off between \(\mu_{max}\) and \(R^{\ast}\), i.e.,

\[ \begin{align} \frac{d^2 \mu_2}{d R^2}< \frac{d^2 \mu_1}{d R^2}<0 \\ \mu_{max,1} > \mu_{max,2} \end{align} \]

Thus, the trade-off can be viewed that opportunist must “consume” var(R) more than gleaner for stable coexistence (Yamamichi & Letten 2022).

Storage effect

Now instead alternating good and bad seasons, we will assume that growth depends unimodally on some external factor such as temperature. If species differ in their optimal temperatures, then the outcome of competition in a constant environment would depend on temperature. If the environment fluctuates so that each species has a time when they’re the best competitor, might they coexist as Hutchinson (1961) suggested? For simplicity, we assume linear functional responses and a closed system as below:

\[\begin{align} \frac{dN_1}{dt} &= (\mu_1 R - m ) N_1 \\ \frac{dN_2}{dt} &= (\mu_2 R - m ) N_2 \\ \frac{dR}{dt} &= (R_{in} - R) - v_{1} R N_1 - v_{2} R N_2 \end{align}\]

where \(\mu_{i}\) is the growth rate, \(v_{i}\) is the uptake rate, and \(R_{in}\) is the input of resource.

The environmental factor, \(T(t)\), which could represent temperature changes in time, could affect either the density independent death rate \(m_i(T)\) or the resource-dependent birth rate \(\mu_i(T)\). We will look at both in turn to see if Hutchinson was correct that environmental variation can sidestep the Competitive Exclusion Principle and allow more than one species to coexist on one limiting resource.

Temporally varying death rate

Here we assume that the death rate mi increases quadratically away from a species-specific optimum temperature \(T_{opt,i}\) as

\[ m_i = m+ \frac{(T_{opt,i} - T)^2}{\sigma ^2} \]

where \(m\) is a baseline temperature-independent death rate and \(\sigma\) measures the width of the temperature response.

#| standalone: true
#| viewerHeight: 800
#| viewerWidth: 900
library(shiny)
library(bslib)
library(plotly)
library(Matrix)

death_rate <- function(m, temp, temp_opt, sigma){
  return(m + (temp_opt - temp)^2 / sigma^2)
}


Sim_rc <- function(tt, mu1, mu2,
                   v1, v2,
                   r1in, 
                   N10, N20, R10, 
                   m,
                   temp, temp_opt1, temp_opt2, sigma
                   ) {
  N1 <- c(N10)
  N2 <- c(N20)
  R1 <- c(R10)
  m1 <- death_rate(m, temp, temp_opt1, sigma)
  m2 <- death_rate(m, temp, temp_opt2, sigma)
  for(ti in 1:tt){
    temp_N1 <- N1[ti]
    temp_N2 <- N2[ti]
    temp_R1 <- R1[ti]
    for(tii in 1:100){
      dN1 <- (mu1 * temp_R1 - m1) * temp_N1 / 100
      dN2 <- (mu2 * temp_R1 - m2) * temp_N2 / 100
      dR1 <- ((r1in - temp_R1) - v1 * temp_N1 - v2 * temp_N2) / 100

      temp_N1 <- max(temp_N1 + dN1, 0)
      temp_N2 <- max(temp_N2 + dN2, 0)
      temp_R1 <- max(temp_R1 + dR1, 0)

    }
    
    N1 <- c(N1, temp_N1)
    N2 <- c(N2, temp_N2)
    
    R1 <- c(R1, temp_R1)
  }
  return(data.frame(N1 = N1, N2 = N2, R1 = R1, cc = 1:(tt+1)))
  
}


# Define UI for app that draws a histogram ----
# Define UI for app that draws a histogram ----
ui <- fluidPage(
  headerPanel(''),
  
  fluidRow(
    column(12, 
           textOutput("text"),
           tags$head(tags$style("#text{color: black;
                                 font-size: 30px;
                                 font-style: italic;
                                 }"
           )
           ),
           plotlyOutput("plot1", width=800, height=280),
           plotlyOutput("plot2", width=800, height=280)
    )
  ), 
  
  fluidRow(
    column(4, 
           div(style="height: 80px;",sliderInput('tempopt1', HTML("T<sub>opt,1</sub>"), -0.2, min = -2., max = 2., step = 0.1)),
           div(style="height: 80px;",sliderInput('tempopt2', HTML("T<sub>opt,2</sub>"), 0.4, min = -2., max = 2., step = 0.1))
    ),
    column(4,
           div(style="height: 80px;", sliderInput('T', HTML("Temperature"), 0.5, min = -1.5, max = 1.5))
    )
  )
  
  
)

server <- function(input, output, session) {
  output$text <- renderText({
    "Temperature-dependent death rate"
  })
  
  
  # sim lv model
  sim_result <- reactive({
    Sim_rc(100, 1.0, 1.0, 1.3, 1.3,
           10, 0.1, 0.1, 1,
           0.1, input$T, input$tempopt1, input$tempopt2, 1
           )
  })
  # browser()
  
  output$plot1 <- renderPlotly({
    T <- seq(-1, 1, 0.01)
    
    m1 <-reactive({
      death_rate(m = 0.1, temp = T, temp_opt = input$tempopt1, sigma = 1)
    })
    
    m2 <-reactive({
      death_rate(m = 0.1, temp = T, temp_opt = input$tempopt2, sigma = 1)
    })
    
    
    gr <- data.frame(T = T, m1 = m1(), m2 = m2())
    # browser()
    p <- plot_ly(data = gr) %>%
      add_trace(x = ~T, y = ~m1, type = 'scatter', mode = 'lines', name = 'm1', line = list(color = 'rgb(205, 12, 24)', width = 4)) %>%
      add_trace(x = ~T, y = ~m2, type = 'scatter', mode = 'lines', name = 'm2', line = list(color = 'rgb(22, 96, 167)', width = 4))
    
    # add vertical line with input$T
    p <- p %>% add_trace(x = c(input$T, input$T), y = c(0, 2), type = 'scatter', mode = 'lines', name = 'Temperature',
                         line = list(color = 'black', width = 4, dash = 'dash'))
    
    # xlim
    # p <- p %>% layout(xaxis = list(range = c(0, 2)),
    #                   yaxis = list(range = c(0, 2)))
    p <- p %>% layout(xaxis = list(title = "Temperature"),yaxis = list(title = "Death rate"))
    
    
    
    p
  })
  
  output$plot2 <- renderPlotly({
    
    # browser()
    p <- plot_ly(data = sim_result()) %>%
      add_trace(x = ~cc, y = ~N1, type = 'scatter', mode = 'lines', name = 'Species 1', line = list(color = 'rgb(205, 12, 24)', width = 4)) %>%
      add_trace(x = ~cc, y = ~N2, type = 'scatter', mode = 'lines', name = 'Species 2', line = list(color = 'rgb(22, 96, 167)', width = 4))
    
    
    # xlim
    # p <- p %>% layout(xaxis = list(range = c(0, 2)),
    #                   yaxis = list(range = c(0, 2)))
    
    p <- p %>% layout(xaxis = list(title = "Time"),yaxis = list(title = "Density"))
    
    
    p
  })
  
}
# Create Shiny app ----
shinyApp(ui = ui, server = server)

So, it looks like the species wins when the temperature is close to its optimal temperature.

Now, we make the temperature change periodically.

\[ T = sin(2\pi t / \tau) \]

#| standalone: true
#| viewerHeight: 800
#| viewerWidth: 900
library(shiny)
library(bslib)
library(plotly)
library(Matrix)

death_rate <- function(m, temp, temp_opt, sigma){
  return(m + (temp_opt - temp)^2 / sigma^2)
}


Sim_rc <- function(tt, mu1, mu2,
                   v1, v2,
                   r1in, 
                   N10, N20, R10, 
                   m,
                   temp, temp_opt1, temp_opt2, sigma, tau
                   ) {
  N1 <- c(N10)
  N2 <- c(N20)
  R1 <- c(R10)

  for(ti in 1:tt){
    temp_N1 <- N1[ti]
    temp_N2 <- N2[ti]
    temp_R1 <- R1[ti]
    for(tii in 1:100){
      temp <- sin(2 * pi * (ti + tii / 100) / tau)
      m1 <- death_rate(m, temp, temp_opt1, sigma)
      m2 <- death_rate(m, temp, temp_opt2, sigma)
      dN1 <- (mu1 * temp_R1 - m1) * temp_N1 / 100
      dN2 <- (mu2 * temp_R1 - m2) * temp_N2 / 100
      dR1 <- ((r1in - temp_R1) - v1 * temp_N1 - v2 * temp_N2) / 100

      temp_N1 <- max(temp_N1 + dN1, 0)
      temp_N2 <- max(temp_N2 + dN2, 0)
      temp_R1 <- max(temp_R1 + dR1, 0)

    }
    
    N1 <- c(N1, temp_N1)
    N2 <- c(N2, temp_N2)
    
    R1 <- c(R1, temp_R1)
  }
  return(data.frame(N1 = N1, N2 = N2, R1 = R1, cc = 1:(tt+1)))
  
}


# Define UI for app that draws a histogram ----
# Define UI for app that draws a histogram ----
ui <- fluidPage(
  headerPanel(''),
  
  fluidRow(
    column(12, 
           textOutput("text"),
           tags$head(tags$style("#text{color: black;
                                 font-size: 30px;
                                 font-style: italic;
                                 }"
           )
           ),
           plotlyOutput("plot1", width=800, height=280),
           plotlyOutput("plot2", width=800, height=280)
    )
  ), 
  
  fluidRow(
    column(4, 
           div(style="height: 80px;",sliderInput('tempopt1', HTML("T<sub>opt,1</sub>"), -0.2, min = -2., max = 2., step = 0.1)),
           div(style="height: 80px;",sliderInput('tempopt2', HTML("T<sub>opt,2</sub>"), 0.4, min = -2., max = 2., step = 0.1))
    ),
    column(4,
           div(style="height: 80px;", sliderInput('T', HTML("Temperature"), 0.5, min = -1.5, max = 1.5)),
           div(style="height: 80px;", sliderInput('tau', HTML("Period"), 3.5, min = 0.1, max = 20))
    )
  )
  
  
)

server <- function(input, output, session) {
  output$text <- renderText({
    "Periodical temperature"
  })
  
  
  # sim lv model
  sim_result <- reactive({
    Sim_rc(100, 1.0, 1.0, 1.3, 1.3,
           10, 0.1, 0.1, 1,
           0.1, input$T, input$tempopt1, input$tempopt2, 1, input$tau
           )
  })
  # browser()
  
  output$plot1 <- renderPlotly({
    tt <- seq(0, 10, 0.01)
    
    temp <- reactive({sin(2 * pi * (tt) / input$tau)})
    
    
    gr <- data.frame(tt = tt, temp = temp())
    # browser()
    p <- plot_ly(data = gr) %>%
      add_trace(x = ~tt, y = ~temp, type = 'scatter', mode = 'lines', name = 'Temperature', line = list(color = 'black', width = 2))
    
    # add horizontal lines for topt1 and topt2
    p <- p %>% add_trace(x = c(0, 10), y = input$tempopt1, type = 'scatter', mode = 'lines', name = 'Topt 1',
                         line = list(color = 'rgb(205, 12, 24)', width = 4, dash = 'dash')) %>%
      add_trace(x = c(0, 10), y = input$tempopt2, type = 'scatter', mode = 'lines', name = 'Topt 2',
                line = list(color = 'rgb(22, 96, 167)', width = 4, dash = 'dash'))

    
    # xlim
    # p <- p %>% layout(xaxis = list(range = c(0, 2)),
    #                   yaxis = list(range = c(0, 2)))
    p <- p %>% layout(xaxis = list(title = "Time"),yaxis = list(title = "Temperature"))
    
    
    
    p
  })
  
  output$plot2 <- renderPlotly({
    
    # browser()
    p <- plot_ly(data = sim_result()) %>%
      add_trace(x = ~cc, y = ~N1, type = 'scatter', mode = 'lines', name = 'Species 1', line = list(color = 'rgb(205, 12, 24)', width = 4)) %>%
      add_trace(x = ~cc, y = ~N2, type = 'scatter', mode = 'lines', name = 'Species 2', line = list(color = 'rgb(22, 96, 167)', width = 4))
    
    
    # xlim
    # p <- p %>% layout(xaxis = list(range = c(0, 2)),
    #                   yaxis = list(range = c(0, 2)))
    
    p <- p %>% layout(xaxis = list(title = "Time"),yaxis = list(title = "Density"))
    
    
    p
  })
  
}
# Create Shiny app ----
shinyApp(ui = ui, server = server)

Can you find a way for the two species coexist by varying parameters? If so, what did it take? Is this coexistence robust?

From the simulation exploration, it looks like whichever species is best competitor on average (its optimal temperature is closer to the mean of the periodically changing temperature) excludes the other — no coexistence.

Temporally varying birth rate

Now we will make the environmental variation affect the resource-dependent birth rate instead, by making the per-resource birth rate \(\mu_i\) a Gaussian function of temperature.

\[ \mu_i = \mu e^{-(T - T_{opt,i})^2 / \sigma^2} \]

#| standalone: true
#| viewerHeight: 800
#| viewerWidth: 900
library(shiny)
library(bslib)
library(plotly)
library(Matrix)

growth_rate <- function(mu, temp, temp_opt, sigma){
  return(mu * exp( -(temp_opt - temp)^2 / sigma^2))
}


Sim_rc <- function(tt, mu1, mu2,
                   v1, v2,
                   r1in, 
                   N10, N20, R10, 
                   m,
                   temp, temp_opt1, temp_opt2, sigma, tau
                   ) {
  N1 <- c(N10)
  N2 <- c(N20)
  R1 <- c(R10)

  for(ti in 1:tt){
    temp_N1 <- N1[ti]
    temp_N2 <- N2[ti]
    temp_R1 <- R1[ti]
    for(tii in 1:100){
      temp <- sin(2 * pi * (ti + tii / 100) / tau)
      mu1_g <- growth_rate(mu1, temp, temp_opt1, sigma)
      mu2_g <- growth_rate(mu2, temp, temp_opt2, sigma)
      dN1 <- (mu1_g * temp_R1 - m) * temp_N1 / 100
      dN2 <- (mu2_g * temp_R1 - m) * temp_N2 / 100
      dR1 <- ((r1in - temp_R1) - v1 * mu1_g * temp_N1 * temp_R1 - v2 *mu2_g  * temp_N2 * temp_R1) / 100

      temp_N1 <- max(temp_N1 + dN1, 0)
      temp_N2 <- max(temp_N2 + dN2, 0)
      temp_R1 <- max(temp_R1 + dR1, 0)

    }
    
    N1 <- c(N1, temp_N1)
    N2 <- c(N2, temp_N2)
    
    R1 <- c(R1, temp_R1)
  }
  return(data.frame(N1 = N1, N2 = N2, R1 = R1, cc = 1:(tt+1)))
  
}


# Define UI for app that draws a histogram ----
# Define UI for app that draws a histogram ----
ui <- fluidPage(
  headerPanel(''),
  
  fluidRow(
    column(12, 
           textOutput("text"),
           tags$head(tags$style("#text{color: black;
                                 font-size: 30px;
                                 font-style: italic;
                                 }"
           )
           ),
           plotlyOutput("plot1", width=700, height=250),
           plotlyOutput("plot2", width=700, height=250)
    )
  ), 
  
  fluidRow(
    column(4, 
           div(style="height: 80px;",sliderInput('tempopt1', HTML("T<sub>opt,1</sub>"), -0.2, min = -2., max = 2., step = 0.1)),
           div(style="height: 80px;",sliderInput('tempopt2', HTML("T<sub>opt,2</sub>"), 0.4, min = -2., max = 2., step = 0.1))
    ),
    column(4,
           div(style="height: 80px;", sliderInput('tau', HTML("Period"), 3.5, min = 0.1, max = 20))
    )
  )
  
  
)

server <- function(input, output, session) {
  output$text <- renderText({
    "Temperature-dependent death rate"
  })
  
  
  # sim lv model
  sim_result <- reactive({
    Sim_rc(300, 1.5, 1.5, 1.3, 1.3,
           10, 0.1, 0.1, 1,
           0.1, input$T, input$tempopt1, input$tempopt2, 1, input$tau
           )
  })
  # browser()
  
  output$plot1 <- renderPlotly({
    ttemp <- seq(-2, 2, 0.01)
    
    mu1 <- reactive({growth_rate(1.0, ttemp, input$tempopt1, 1)})
    mu2 <- reactive({growth_rate(1.0, ttemp, input$tempopt2, 1)})
    
    gr <- data.frame(ttemp = ttemp, mu1 = mu1(), mu2 = mu2())
    # browser()
    p <- plot_ly(data = gr) %>%
      add_trace(x = ~ttemp, y = ~mu1, type = 'scatter', mode = 'lines', name = 'Growth rate 1', line = list(color = 'rgb(205, 12, 24)', width = 4)) %>%
      add_trace(x = ~ttemp, y = ~mu2, type = 'scatter', mode = 'lines', name = 'Growth rate 2', line = list(color = 'rgb(22, 96, 167)', width = 4))
    
    # add horizontal lines for topt1 and topt2
    p <- p %>% add_trace(x = 0, y = c(0, 2), type = 'scatter', mode = 'lines', name = 'Temperature',
                         line = list(color = 'black', width = 4, dash = 'dash'))

    
    # xlim
    # p <- p %>% layout(xaxis = list(range = c(0, 2)),
    #                   yaxis = list(range = c(0, 2)))
    p <- p %>% layout(xaxis = list(title = "Temperature"),yaxis = list(title = ""))
    
    
    
    p
  })
  
  output$plot2 <- renderPlotly({
    
    # browser()
    p <- plot_ly(data = sim_result()) %>%
      add_trace(x = ~cc, y = ~N1, type = 'scatter', mode = 'lines', name = 'Species 1', line = list(color = 'rgb(205, 12, 24)', width = 4)) %>%
      add_trace(x = ~cc, y = ~N2, type = 'scatter', mode = 'lines', name = 'Species 2', line = list(color = 'rgb(22, 96, 167)', width = 4))
    
    
    # xlim
    # p <- p %>% layout(xaxis = list(range = c(0, 2)),
    #                   yaxis = list(range = c(0, 2)))
    
    p <- p %>% layout(xaxis = list(title = "Time"),yaxis = list(title = "Density"))
    
    
    p
  })
  
}
# Create Shiny app ----
shinyApp(ui = ui, server = server)

So, we found that the two species are possible to coexist when the growth rate is varying. Why is that? We can analyze the dynamical system by studying the average of the change of the density.

\[ \overline{\frac{1}{N_i}\frac{dN_i}{dt}} = \overline{\mu_i R - m} = \overline{\mu_i R} - \overline{m}=0 \]

If only the death rate is changing, not the growth rate, we have

\[ \overline{\frac{1}{N_i}\frac{dN_i}{dt}} = \overline{\mu_i R - m} = \mu_i\overline{ R} - \overline{m}=0 \]

which means that species are competing for the average resource level. We can compute the \(R^{\ast}\) as

\[ R^{\ast} = \frac{\overline{m}}{\mu} \]

So, the one with a lower \(R^{\ast}\) will win in the competition.

However, if the growth rate is changing, we have

\[ \overline{\frac{1}{N_i}\frac{dN_i}{dt}} = \overline{\mu_i R - m} = \overline{\mu_i R} - m=\overline{\mu_i} \overline{ R} + Cov(\mu_i, R) - m \]

The covariance term \(Cov(\mu_i, R)\) can be positive or negative, depending on the correlation between the growth rate and the resource level. If the growth rate is positively correlated with the resource level, the species will be favored by the variable environment. This is the so-called storage effect (Chesson 2000).

What’s the difference?

Variation in density-independent term (mortality) doesn’t generate \(Cov(\mu, R)\) required for the storage effect;
Variation in density-dependent term (births) does;
Interaction between resource-dependence (competition) and environmental variation is key to storage effect.

Invasion analysis

We can also use the invasion analysis to study the coexistence of two species. The invasion fitness of a rare mutant of species 1 in a resident population of species 2 is given by

\[ \lambda_{inv, res} = \overline{\mu_{inv}} \overline{ R_{res}} + Cov(\mu_{inv}, R_{res}) - m_{inv}\\ \lambda_{res, res} = \overline{\mu_{res}} \overline{ R_{res}} + Cov(\mu_{res}, R_{res}) - m_{res} = 0. \]

We can compare term by term of these two invasion rates

\[ \begin{align} \lambda_{inv, res} &= (\overline{\mu_{inv}} - \overline{\mu_{res}}) \overline{ R_{res}} - ( m_{inv} - m_{res}) \\ &+ (Cov(\mu_{inv}, R_{res}) - Cov(\mu_{res}, R_{res}) ) \end{align} \]

which means that the invasion rate can be decompsed to the difference in the growth rate, the difference in the death rate, and the difference in the covariance between the growth rate and the resource level.

References

Yamamichi, Masato, and Andrew D. Letten. “Extending the Gleaner–Opportunist Trade-Off.” Journal of Animal Ecology 91, no. 11 (2022): 2163-70. https://doi.org/https://doi.org/10.1111/1365-2656.13813. https://besjournals.onlinelibrary.wiley.com/doi/abs/10.1111/1365-2656.13813.

Chesson, Peter. “Mechanisms of Maintenance of Species Diversity.” Annual Review of Ecology and Systematics 31, no. 1 (2000): 343-66. https://doi.org/10.1146/annurev.ecolsys.31.1.343. https://www.annualreviews.org/doi/abs/10.1146/annurev.ecolsys.31.1.343.

Chesson, P. “Multispecies Competition in Variable Environments.” Theoretical Population Biology 45, no. 3 (1994/06/01/ 1994): 227-76. https://doi.org/https://doi.org/10.1006/tpbi.1994.1013. https://www.sciencedirect.com/science/article/pii/S0040580984710136.

Hutchinson, G. E. “The Paradox of the Plankton.” The American Naturalist 95, no. 882 (1961): 137-45. http://www.jstor.org/stable/2458386.

Armstrong, Robert A., and Richard McGehee. “Competitive Exclusion.” The American Naturalist 115, no. 2 (1980): 151-70. http://www.jstor.org/stable/2460592.